Using convolutional neural nets to detect facial keypoints tutorial

Prerequisites

You don't need to type the code and execute it yourself if you just want to follow along. But here's the installation instructions for those who have access to a CUDA-capable GPU and want to run the experiments themselves.

I assume you have the CUDA toolkit, Python 2.7.x, numpy, pandas, matplotlib, and scikit-learn installed. To install the remaining dependencies, such as Lasagne and Theano run this command:

pip install -r https://raw.githubusercontent.com/dnouri/kfkd-tutorial/master/requirements.txt

(Note that for sake of brevity, I'm not including commands to create a virtualenv and activate it. But you should.)

If everything worked well, you should be able to find the src/lasagne/examples/ directory in your virtualenv and run the MNIST example. This is sort of the "Hello, world" of neural nets. There's ten classes, one for each digit between 0 and 9, and the input is grayscale images of handwritten digits of size 28x28.

cd src/lasagne/examples/
python mnist.py

This command will start printing out stuff after thirty seconds or so. The reason it takes a while is that Lasagne uses Theano to do the heavy lifting; Theano in turn is a "optimizing GPU-meta-programming code generating array oriented optimizing math compiler in Python," and it will generate C code that needs to be compiled before training can happen. Luckily, we have to pay the price for this overhead only on the first run.

Once training starts, you'll see output like this:

Epoch 1 of 500
  training loss:            1.352731
  validation loss:          0.466565
  validation accuracy:              87.70 %
Epoch 2 of 500
  training loss:            0.591704
  validation loss:          0.326680
  validation accuracy:              90.64 %
Epoch 3 of 500
  training loss:            0.464022
  validation loss:          0.275699
  validation accuracy:              91.98 %
...

If you let training run long enough, you'll notice that after about 75 epochs, it'll have reached a test accuracy of around 98%.

If you have a GPU, you'll want to configure Theano to use it. You'll want to create a ~/.theanorc file in your home directory that looks something like this:

[global]
floatX = float32
device = gpu0

[lib]
cnmem = 1

(Should any of the instructions in this tutorial not work for you, submit a bug report here.)

The data

The training dataset for the Facial Keypoint Detection challenge consists of 7,049 96x96 gray-scale images. For each image, we're supposed learn to find the correct position (the x and y coordinates) of 15 keypoints, such as left_eye_center, right_eye_outer_corner, mouth_center_bottom_lip, and so on.

An example of one of the faces with three keypoints marked.

An interesting twist with the dataset is that for some of the keypoints we only have about 2,000 labels, while other keypoints have more than 7,000 labels available for training.

Let's write some Python code that loads the data from the CSV files provided. We'll write a function that can load both the training and the test data. These two datasets differ in that the test data doesn't contain the target values; it's the goal of the challenge to predict these. Here's our load() function:

# file kfkd.py
import os

import numpy as np
from pandas.io.parsers import read_csv
from sklearn.utils import shuffle


FTRAIN = '~/data/kaggle-facial-keypoint-detection/training.csv'
FTEST = '~/data/kaggle-facial-keypoint-detection/test.csv'


def load(test=False, cols=None):
    """Loads data from FTEST if *test* is True, otherwise from FTRAIN.
    Pass a list of *cols* if you're only interested in a subset of the
    target columns.
    """
    fname = FTEST if test else FTRAIN
    df = read_csv(os.path.expanduser(fname))  # load pandas dataframe

    # The Image column has pixel values separated by space; convert
    # the values to numpy arrays:
    df['Image'] = df['Image'].apply(lambda im: np.fromstring(im, sep=' '))

    if cols:  # get a subset of columns
        df = df[list(cols) + ['Image']]

    print(df.count())  # prints the number of values for each column
    df = df.dropna()  # drop all rows that have missing values in them

    X = np.vstack(df['Image'].values) / 255.  # scale pixel values to [0, 1]
    X = X.astype(np.float32)

    if not test:  # only FTRAIN has any target columns
        y = df[df.columns[:-1]].values
        y = (y - 48) / 48  # scale target coordinates to [-1, 1]
        X, y = shuffle(X, y, random_state=42)  # shuffle train data
        y = y.astype(np.float32)
    else:
        y = None

    return X, y


X, y = load()
print("X.shape == {}; X.min == {:.3f}; X.max == {:.3f}".format(
    X.shape, X.min(), X.max()))
print("y.shape == {}; y.min == {:.3f}; y.max == {:.3f}".format(
    y.shape, y.min(), y.max()))

It's not necessary that you go through every single detail of this function. But let's take a look at what the script above outputs:

$ python kfkd.py
left_eye_center_x            7034
left_eye_center_y            7034
right_eye_center_x           7032
right_eye_center_y           7032
left_eye_inner_corner_x      2266
left_eye_inner_corner_y      2266
left_eye_outer_corner_x      2263
left_eye_outer_corner_y      2263
right_eye_inner_corner_x     2264
right_eye_inner_corner_y     2264
...
mouth_right_corner_x         2267
mouth_right_corner_y         2267
mouth_center_top_lip_x       2272
mouth_center_top_lip_y       2272
mouth_center_bottom_lip_x    7014
mouth_center_bottom_lip_y    7014
Image                        7044
dtype: int64
X.shape == (2140, 9216); X.min == 0.000; X.max == 1.000
y.shape == (2140, 30); y.min == -0.920; y.max == 0.996

First it's printing a list of all columns in the CSV file along with the number of available values for each. So while we have an Image for all rows in the training data, we only have 2,267 values for mouth_right_corner_x and so on.

load() returns a tuple (X, y) where y is the target matrix. y has shape n x m with n being the number of samples in the dataset that have all m keypoints. Dropping all rows with missing values is what this line does:

df = df.dropna()  # drop all rows that have missing values in them

The script's output y.shape == (2140, 30) tells us that there's only 2,140 images in the dataset that have all 30 target values present. Initially, we'll train with these 2,140 samples only. Which leaves us with many more input dimensions (9,216) than samples; an indicator that overfitting might become a problem. Let's see. Of course it's a bad idea to throw away 70% of the training data just like that, and we'll talk about this later on.

Another feature of the load() function is that it scales the intensity values of the image pixels to be in the interval [0, 1], instead of 0 to 255. The target values (x and y coordinates) are scaled to [-1, 1]; before they were between 0 to 95.

First model: a single hidden layer

Now that we're done with the legwork of loading the data, let's use Lasagne and create a neural net with a single hidden layer. We'll start with the code:

# add to kfkd.py
from lasagne import layers
from lasagne.updates import nesterov_momentum
from nolearn.lasagne import NeuralNet

net1 = NeuralNet(
    layers=[  # three layers: one hidden layer
        ('input', layers.InputLayer),
        ('hidden', layers.DenseLayer),
        ('output', layers.DenseLayer),
        ],
    # layer parameters:
    input_shape=(None, 9216),  # 96x96 input pixels per batch
    hidden_num_units=100,  # number of units in hidden layer
    output_nonlinearity=None,  # output layer uses identity function
    output_num_units=30,  # 30 target values

    # optimization method:
    update=nesterov_momentum,
    update_learning_rate=0.01,
    update_momentum=0.9,

    regression=True,  # flag to indicate we're dealing with regression problem
    max_epochs=400,  # we want to train this many epochs
    verbose=1,
    )

X, y = load()
net1.fit(X, y)

We use quite a few parameters to initialize the NeuralNet. Let's walk through them. First there's the three layers and their parameters:

    layers=[  # three layers: one hidden layer
        ('input', layers.InputLayer),
        ('hidden', layers.DenseLayer),
        ('output', layers.DenseLayer),
        ],
    # layer parameters:
    input_shape=(None, 9216),  # 96x96 input pixels per batch
    hidden_num_units=100,  # number of units in hidden layer
    output_nonlinearity=None,  # output layer uses identity function
    output_num_units=30,  # 30 target values

Here we define the input layer, the hidden layer and the output layer. In parameter layers, we name and specify the type of each layer, and their order. Parameters input_shape, hidden_num_units, output_nonlinearity, and output_num_units are each parameters for specific layers; they refer to the layer by their prefix, such that input_shape defines the shape parameter of the input layer, hidden_num_units defines the hidden layer's num_units and so on. (It may seem a little odd that we have to specify the parameters like this, but the upshot is it buys us better compatibility with scikit-learn's pipeline and parameter search features.)

We set the first dimension of input_shape to None. This translates to a variable batch size.

We set the output_nonlinearity to None explicitly. Thus, the output units' activations become just a linear combination of the activations in the hidden layer.

The default nonlinearity used by DenseLayer is the rectifier, which is simply max(0, x). It's the most popular choice of activation function these days. By not explicitly setting hidden_nonlinearity, we're choosing the rectifier as the activiation function of our hidden layer.

The neural net's weights are initialized from a uniform distribution with a cleverly chosen interval. That is, Lasagne figures out this interval for us, using "Glorot-style" initialization.

There's a few more parameters. All parameters starting with update parametrize the update function, or optimization method. The update function will update the weights of our network after each batch. We'll use the nesterov_momentum gradient descent optimization method to do the job. There's a number of other methods that Lasagne implements, such as adagrad and rmsprop. We choose nesterov_momentum because it has proven to work very well for a large number of problems.

    # optimization method:
    update=nesterov_momentum,
    update_learning_rate=0.01,
    update_momentum=0.9,

The update_learning_rate defines how large we want the steps of the gradient descent updates to be. We'll talk a bit more about the learning_rate and momentum parameters later on. For now, it's enough to just use these "sane defaults."

Comparison of a few optimization methods (animation by Alec Radford). The star denotes the global minimum on the error surface. Notice that stochastic gradient descent (SGD) without momentum is the slowest method to converge in this example. We're using Nesterov's Accelerated Gradient Descent (NAG) throughout this tutorial.

In our definition of NeuralNet we didn't specify an objective function to minimize. There's again a default for that; for regression problems it's the mean squared error (MSE).

The last set of parameters declare that we're dealing with a regression problem (as opposed to classification), that 400 is the number of epochs we're willing to train, and that we want to print out information during training by setting verbose=1:

  regression=True,  # flag to indicate we're dealing with regression problem
  max_epochs=400,  # we want to train this many epochs
  verbose=1,

Finally, the last two lines in our script load the data, just as before, and then train the neural net with it:

X, y = load()
net1.fit(X, y)

Running these two lines will output a table that grows one row per training epoch. In each row, we'll see the current loss (MSE) on the train set and on the validation set and the ratio between the two. NeuralNet automatically splits the data provided in X into a training and a validation set, using 20% of the samples for validation. (You can adjust this ratio by overriding the eval_size=0.2 parameter.)

$ python kfkd.py
...
  InputLayer          (None, 9216)            produces    9216 outputs
  DenseLayer          (None, 100)             produces     100 outputs
  DenseLayer          (None, 30)              produces      30 outputs

 Epoch  |  Train loss  |  Valid loss  |  Train / Val
--------|--------------|--------------|----------------
     1  |    0.105418  |    0.031085  |     3.391261
     2  |    0.020353  |    0.019294  |     1.054894
     3  |    0.016118  |    0.016918  |     0.952734
     4  |    0.014187  |    0.015550  |     0.912363
     5  |    0.013329  |    0.014791  |     0.901199
...
   200  |    0.003250  |    0.004150  |     0.783282
   201  |    0.003242  |    0.004141  |     0.782850
   202  |    0.003234  |    0.004133  |     0.782305
   203  |    0.003225  |    0.004126  |     0.781746
   204  |    0.003217  |    0.004118  |     0.781239
   205  |    0.003209  |    0.004110  |     0.780738
...
   395  |    0.002259  |    0.003269  |     0.690925
   396  |    0.002256  |    0.003264  |     0.691164
   397  |    0.002254  |    0.003264  |     0.690485
   398  |    0.002249  |    0.003259  |     0.690303
   399  |    0.002247  |    0.003260  |     0.689252
   400  |    0.002244  |    0.003255  |     0.689606

On a reasonably fast GPU, we're able to train for 400 epochs in under a minute. Notice that the validation loss keeps improving until the end. (If you let it train longer, it will improve a little more.)

Now how good is a validation loss of 0.0032? How does it compare to the challenge's benchmark or the other entries in the leaderboard? Remember that we divided the target coordinates by 48 when we scaled them to be in the interval [-1, 1]. Thus, to calculate the root-mean-square error, as that's what's used in the challenge's leaderboard, based on our MSE loss of 0.003255, we'll take the square root and multiply by 48 again:

>>> import numpy as np
>>> np.sqrt(0.003255) * 48
2.7385251505144153

This is reasonable proxy for what our score would be on the Kaggle leaderboard; at the same time it's assuming that the subset of the data that we chose to train with follows the same distribution as the test set, which isn't really the case. My guess is that the score is good enough to earn us a top ten place in the leaderboard at the time of writing. Certainly not a bad start! (And for those of you that are crying out right now because of the lack of a proper test set: don't.)

Testing it out

The net1 object actually keeps a record of the data that it prints out in the table. We can access that record through the train_history_ attribute. Let's draw those two curves:

train_loss = np.array([i["train_loss"] for i in net1.train_history_])
valid_loss = np.array([i["valid_loss"] for i in net1.train_history_])
pyplot.plot(train_loss, linewidth=3, label="train")
pyplot.plot(valid_loss, linewidth=3, label="valid")
pyplot.grid()
pyplot.legend()
pyplot.xlabel("epoch")
pyplot.ylabel("loss")
pyplot.ylim(1e-3, 1e-2)
pyplot.yscale("log")
pyplot.show()

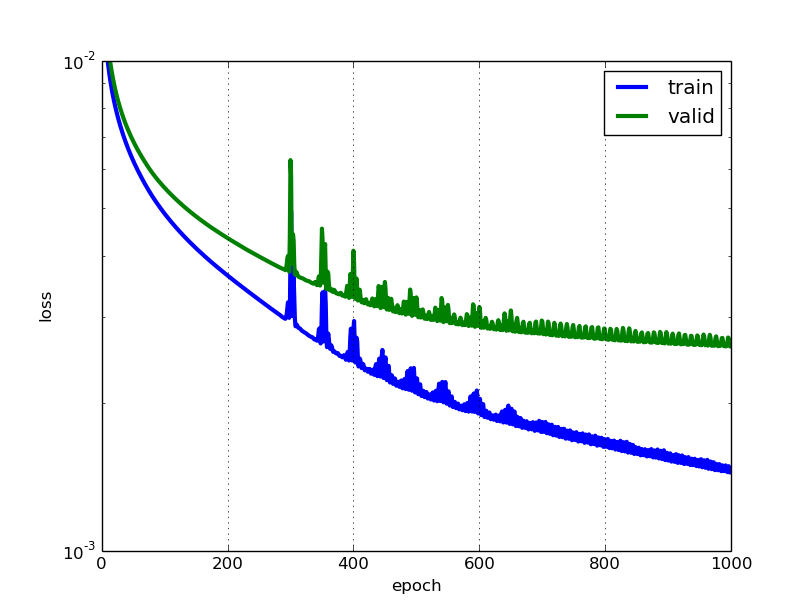
We can see that our net overfits, but it's not that bad. In particular, we don't see a point where the validation error gets worse again, thus it doesn't appear that early stopping, a technique that's commonly used to avoid overfitting, would be very useful at this point. Notice that we didn't use any regularization whatsoever, apart from choosing a small number of neurons in the hidden layer, a setting that will keep overfitting somewhat in control.

How do the net's predictions look like, then? Let's pick a few examples from the test set and check:

def plot_sample(x, y, axis):
    img = x.reshape(96, 96)
    axis.imshow(img, cmap='gray')
    axis.scatter(y[0::2] * 48 + 48, y[1::2] * 48 + 48, marker='x', s=10)

X, _ = load(test=True)
y_pred = net1.predict(X)

fig = pyplot.figure(figsize=(6, 6))
fig.subplots_adjust(
    left=0, right=1, bottom=0, top=1, hspace=0.05, wspace=0.05)

for i in range(16):
    ax = fig.add_subplot(4, 4, i + 1, xticks=[], yticks=[])
    plot_sample(X[i], y_pred[i], ax)

pyplot.show()

Our first model's predictions on 16 samples taken from the test set.

The predictions look reasonable, but sometimes they are quite a bit off. Let's try and do a bit better.

Second model: convolutions

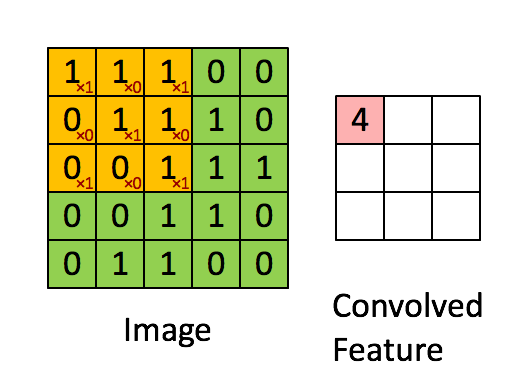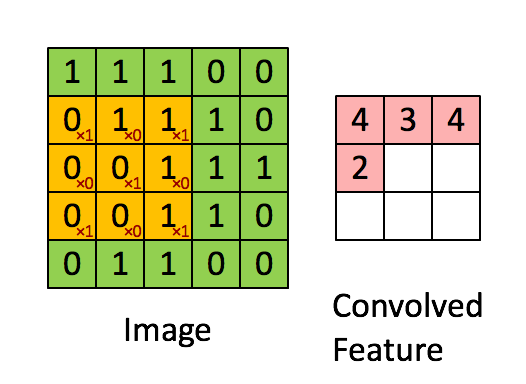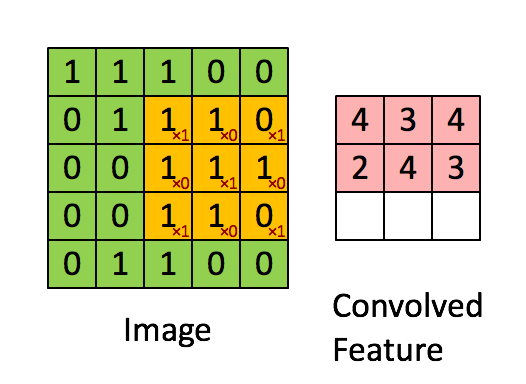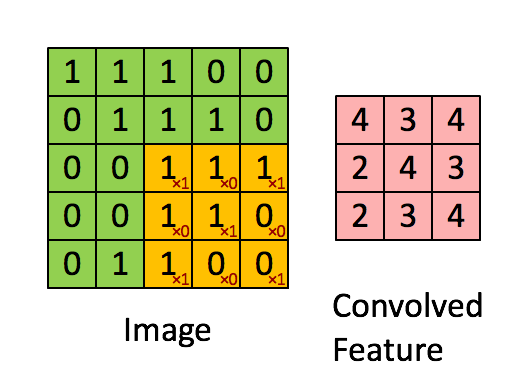
The convolution operation. (Animation taken from the Stanford deep learning tutorial.)

LeNet5-style convolutional neural nets are at the heart of deep learning's recent breakthrough in computer vision. Convolutional layers are different to fully connected layers; they use a few tricks to reduce the number of parameters that need to be learned, while retaining high expressiveness. These are:

• local connectivity: neurons are connected only to a subset of neurons in the previous layer,
• weight sharing: weights are shared between a subset of neurons in the convolutional layer (these neurons form what's called a feature map),
• pooling: static subsampling of inputs.

Illustration of local connectivity and weight sharing. (Taken from the deeplearning.net tutorial.)

Units in a convolutional layer actually connect to a 2-d patch of neurons in the previous layer, a prior that lets them exploit the 2-d structure in the input.

When using convolutional layers in Lasagne, we have to prepare the input data such that each sample is no longer a flat vector of 9,216 pixel intensities, but a three-dimensional matrix with shape (c, 0, 1), where c is the number of channels (colors), and 0 and 1 correspond to the x and y dimensions of the input image. In our case, the concrete shape will be (1, 96, 96), because we're dealing with a single (gray) color channel only.

A function load2d that wraps the previously written load and does the necessary transformations is easily coded:

def load2d(test=False, cols=None):
    X, y = load(test=test)
    X = X.reshape(-1, 1, 96, 96)
    return X, y

We'll build a convolutional neural net with three convolutional layers and two fully connected layers. Each conv layer is followed by a 2x2 max-pooling layer. Starting with 32 filters, we double the number of filters with every conv layer. The densely connected hidden layers both have 500 units.

There's again no regularization in the form of weight decay or dropout. It turns out that using very small convolutional filters, such as our 3x3 and 2x2 filters, is again a pretty good regularizer by itself.

Let's write down the code:

net2 = NeuralNet(
    layers=[
        ('input', layers.InputLayer),
        ('conv1', layers.Conv2DLayer),
        ('pool1', layers.MaxPool2DLayer),
        ('conv2', layers.Conv2DLayer),
        ('pool2', layers.MaxPool2DLayer),
        ('conv3', layers.Conv2DLayer),
        ('pool3', layers.MaxPool2DLayer),
        ('hidden4', layers.DenseLayer),
        ('hidden5', layers.DenseLayer),
        ('output', layers.DenseLayer),
        ],
    input_shape=(None, 1, 96, 96),
    conv1_num_filters=32, conv1_filter_size=(3, 3), pool1_pool_size=(2, 2),
    conv2_num_filters=64, conv2_filter_size=(2, 2), pool2_pool_size=(2, 2),
    conv3_num_filters=128, conv3_filter_size=(2, 2), pool3_pool_size=(2, 2),
    hidden4_num_units=500, hidden5_num_units=500,
    output_num_units=30, output_nonlinearity=None,

    update_learning_rate=0.01,
    update_momentum=0.9,

    regression=True,
    max_epochs=1000,
    verbose=1,
    )

X, y = load2d()  # load 2-d data
net2.fit(X, y)

# Training for 1000 epochs will take a while.  We'll pickle the
# trained model so that we can load it back later:
import cPickle as pickle
with open('net2.pickle', 'wb') as f:
    pickle.dump(net2, f, -1)

Training this neural net is much more computationally costly than the first one we trained. It takes around 15x as long to train; those 1000 epochs take more than 20 minutes on even a powerful GPU.

However, our patience is rewarded with what's already a much better model than the one we had before. Let's take a look at the output when running the script. First comes the list of layers with their output shapes. Note that the first conv layer produces 32 output images of size (94, 94), that's one 94x94 output image per filter:

InputLayer            (None, 1, 96, 96)       produces    9216 outputs
Conv2DCCLayer         (None, 32, 94, 94)      produces  282752 outputs
MaxPool2DCCLayer      (None, 32, 47, 47)      produces   70688 outputs
Conv2DCCLayer         (None, 64, 46, 46)      produces  135424 outputs
MaxPool2DCCLayer      (None, 64, 23, 23)      produces   33856 outputs
Conv2DCCLayer         (None, 128, 22, 22)     produces   61952 outputs
MaxPool2DCCLayer      (None, 128, 11, 11)     produces   15488 outputs
DenseLayer            (None, 500)             produces     500 outputs
DenseLayer            (None, 500)             produces     500 outputs
DenseLayer            (None, 30)              produces      30 outputs

What follows is the same table that we saw with the first example, with train and validation error over time:

 Epoch  |  Train loss  |  Valid loss  |  Train / Val
--------|--------------|--------------|----------------
     1  |    0.111763  |    0.042740  |     2.614934
     2  |    0.018500  |    0.009413  |     1.965295
     3  |    0.008598  |    0.007918  |     1.085823
     4  |    0.007292  |    0.007284  |     1.001139
     5  |    0.006783  |    0.006841  |     0.991525
...
   500  |    0.001791  |    0.002013  |     0.889810
   501  |    0.001789  |    0.002011  |     0.889433
   502  |    0.001786  |    0.002009  |     0.889044
   503  |    0.001783  |    0.002007  |     0.888534
   504  |    0.001780  |    0.002004  |     0.888095
   505  |    0.001777  |    0.002002  |     0.887699
...
   995  |    0.001083  |    0.001568  |     0.690497
   996  |    0.001082  |    0.001567  |     0.690216
   997  |    0.001081  |    0.001567  |     0.689867
   998  |    0.001080  |    0.001567  |     0.689595
   999  |    0.001080  |    0.001567  |     0.689089
  1000  |    0.001079  |    0.001566  |     0.688874

Quite a nice improvement over the first network. Our RMSE is looking pretty good, too:

>>> np.sqrt(0.001566) * 48
1.8994904579913006

We can compare the predictions of the two networks using one of the more problematic samples in the test set:

sample1 = load(test=True)[0][6:7]
sample2 = load2d(test=True)[0][6:7]
y_pred1 = net1.predict(sample1)[0]
y_pred2 = net2.predict(sample2)[0]

fig = pyplot.figure(figsize=(6, 3))
ax = fig.add_subplot(1, 2, 1, xticks=[], yticks=[])
plot_sample(sample1[0], y_pred1, ax)
ax = fig.add_subplot(1, 2, 2, xticks=[], yticks=[])
plot_sample(sample1[0], y_pred2, ax)
pyplot.show()

The predictions of net1 on the left compared to the predictions of net2.

And then let's compare the learning curves of the first and the second network:

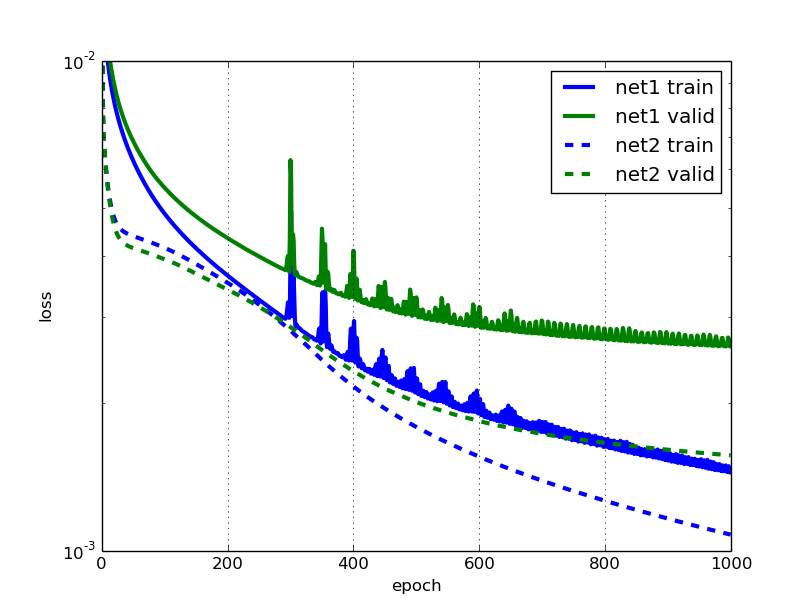
This looks pretty good, I like the smoothness of the new error curves. But we do notice that towards the end, the validation error of net2 flattens out much more quickly than the training error. I bet we could improve that by using more training examples. What if we flipped the input images horizontically; would we be able to improve training by doubling the amount of training data this way?

Data augmentation

An overfitting net can generally be made to perform better by using more training data. (And if your unregularized net does not overfit, you should probably make it larger.)

Data augmentation lets us artificially increase the number of training examples by applying transformations, adding noise etc. That's obviously more economic than having to go out and collect more examples by hand. Augmentation is a very useful tool to have in your deep learning toolbox.

We mentioned batch iterators already briefly. It is the batch iterator's job to take a matrix of samples, and split it up in batches, in our case of size 128. While it does the splitting, the batch iterator can also apply transformations to the data on the fly. So to produce those horizontal flips, we don't actually have to double the amount of training data in the input matrix. Rather, we will just perform the horizontal flips with 50% chance while we're iterating over the data. This is convenient, and for some problems it allows us to produce an infinite number of examples, without blowing up the memory usage. Also, transformations to the input images can be done while the GPU is busy processing a previous batch, so they come at virtually no cost.

Flipping the images horizontically is just a matter of using slicing:

X, y = load2d()
X_flipped = X[:, :, :, ::-1]  # simple slice to flip all images

# plot two images:
fig = pyplot.figure(figsize=(6, 3))
ax = fig.add_subplot(1, 2, 1, xticks=[], yticks=[])
plot_sample(X[1], y[1], ax)
ax = fig.add_subplot(1, 2, 2, xticks=[], yticks=[])
plot_sample(X_flipped[1], y[1], ax)
pyplot.show()

Left shows the original image, right is the flipped image.

In the picture on the right, notice that the target value keypoints aren't aligned with the image anymore. Since we're flipping the images, we'll have to make sure we also flip the target values. To do this, not only do we have to flip the coordinates, we'll also have to swap target value positions; that's because the flipped left_eye_center_x no longer points to the left eye in our flipped image; now it corresponds to right_eye_center_x. Some points like nose_tip_y are not affected. We'll define a tuple flip_indices that holds the information about which columns in the target vector need to swap places when we flip the image horizontically. Remember the list of columns was:

left_eye_center_x            7034
left_eye_center_y            7034
right_eye_center_x           7032
right_eye_center_y           7032
left_eye_inner_corner_x      2266
left_eye_inner_corner_y      2266
...

Since left_eye_center_x will need to swap places with right_eye_center_x, we write down the tuple (0, 2). Also left_eye_center_y needs to swap places: with right_eye_center_y. Thus we write down (1, 3), and so on. In the end, we have:

flip_indices = [
    (0, 2), (1, 3),
    (4, 8), (5, 9), (6, 10), (7, 11),
    (12, 16), (13, 17), (14, 18), (15, 19),
    (22, 24), (23, 25),
    ]

# Let's see if we got it right:
df = read_csv(os.path.expanduser(FTRAIN))
for i, j in flip_indices:
    print("# {} -> {}".format(df.columns[i], df.columns[j]))

# this prints out:
# left_eye_center_x -> right_eye_center_x
# left_eye_center_y -> right_eye_center_y
# left_eye_inner_corner_x -> right_eye_inner_corner_x
# left_eye_inner_corner_y -> right_eye_inner_corner_y
# left_eye_outer_corner_x -> right_eye_outer_corner_x
# left_eye_outer_corner_y -> right_eye_outer_corner_y
# left_eyebrow_inner_end_x -> right_eyebrow_inner_end_x
# left_eyebrow_inner_end_y -> right_eyebrow_inner_end_y
# left_eyebrow_outer_end_x -> right_eyebrow_outer_end_x
# left_eyebrow_outer_end_y -> right_eyebrow_outer_end_y
# mouth_left_corner_x -> mouth_right_corner_x
# mouth_left_corner_y -> mouth_right_corner_y

Our batch iterator implementation will derive from the default BatchIterator class and override the transform() method only. Let's see how it looks like when we put it all together:

from nolearn.lasagne import BatchIterator

class FlipBatchIterator(BatchIterator):
    flip_indices = [
        (0, 2), (1, 3),
        (4, 8), (5, 9), (6, 10), (7, 11),
        (12, 16), (13, 17), (14, 18), (15, 19),
        (22, 24), (23, 25),
        ]

    def transform(self, Xb, yb):
        Xb, yb = super(FlipBatchIterator, self).transform(Xb, yb)

        # Flip half of the images in this batch at random:
        bs = Xb.shape[0]
        indices = np.random.choice(bs, bs / 2, replace=False)
        Xb[indices] = Xb[indices, :, :, ::-1]

        if yb is not None:
            # Horizontal flip of all x coordinates:
            yb[indices, ::2] = yb[indices, ::2] * -1

            # Swap places, e.g. left_eye_center_x -> right_eye_center_x
            for a, b in self.flip_indices:
                yb[indices, a], yb[indices, b] = (
                    yb[indices, b], yb[indices, a])

        return Xb, yb

To use this batch iterator for training, we'll pass it as the batch_iterator_train argument to NeuralNet. Let's define net3, a network that looks exactly the same as net2 except for these lines at the very end:

net3 = NeuralNet(
    # ...
    regression=True,
    batch_iterator_train=FlipBatchIterator(batch_size=128),
    max_epochs=3000,
    verbose=1,
    )

Now we're passing our FlipBatchIterator, but we've also tripled the number of epochs to train. While each one of our training epochs will still look at the same number of examples as before (after all, we haven't changed the size of X), it turns out that training nevertheless takes quite a bit longer when we use our transforming FlipBatchIterator. This is because what the network learns generalizes better this time, and it's arguably harder to learn things that generalize than to overfit.

So this will take maybe take an hour to train. Let's make sure we pickle the model at the end of training, and then we're ready to go fetch some tea and biscuits. Or maybe do the laundry:

net3.fit(X, y)

import cPickle as pickle
with open('net3.pickle', 'wb') as f:
    pickle.dump(net3, f, -1)

$ python kfkd.py
...
 Epoch  |  Train loss  |  Valid loss  |  Train / Val
--------|--------------|--------------|----------------
...
   500  |    0.002238  |    0.002303  |     0.971519
...
  1000  |    0.001365  |    0.001623  |     0.841110
  1500  |    0.001067  |    0.001457  |     0.732018
  2000  |    0.000895  |    0.001369  |     0.653721
  2500  |    0.000761  |    0.001320  |     0.576831
  3000  |    0.000678  |    0.001288  |     0.526410

Comparing the learning with that of net2, we notice that the error on the validation set after 3000 epochs is indeed about 5% smaller for the data augmented net. We can see how net2 stops learning anything useful after 2000 or so epochs, and gets pretty noisy, while net3 continues to improve its validation error throughout, though slowly.

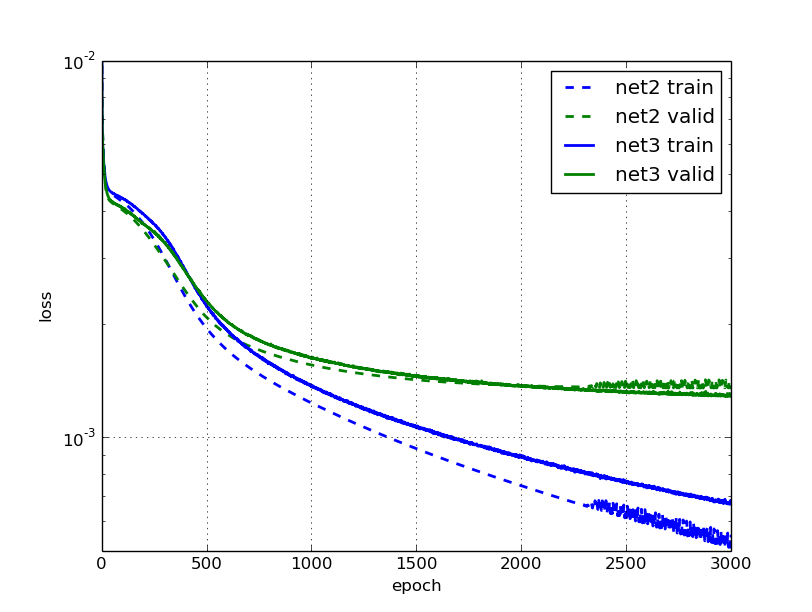
Still seems like a lot of work for only a small gain? We'll find out if it was worth it in the next secion.

Changing learning rate and momentum over time

What's annoying about our last model is that it took already an hour to train it, and it's not exactly inspiring to have to wait for your experiment's results for so long. In this section, we'll talk about a combination of two tricks to fix that and make the net train much faster again.

An intuition behind starting with a higher learning rate and decreasing it during the course of training is this: As we start training, we're far away from the optimum, and we want to take big steps towards it and learn quickly. But the closer we get to the optimum, the lighter we want to step. It's like taking the train home, but when you enter your door you do it by foot, not by train.

On the importance of initialization and momentum in deep learning is the title of a talk and a paper by Ilya Sutskever et al. It's there that we learn about another useful trick to boost deep learning: namely increasing the optimization method's momentum parameter during training.

Remember that in our previous model, we initialized learning rate and momentum with a static 0.01 and 0.9 respectively. Let's change that such that the learning rate decreases linearly with the number of epochs, while we let the momentum increase.

NeuralNet allows us to update parameters during training using the on_epoch_finished hook. We can pass a function to on_epoch_finished and it'll be called whenever an epoch is finished. However, before we can assign new values to update_learning_rate and update_momentum on the fly, we'll have to change these two parameters to become Theano shared variables. Thankfully, that's pretty easy:

import theano

def float32(k):
    return np.cast['float32'](k)

net4 = NeuralNet(
    # ...
    update_learning_rate=theano.shared(float32(0.03)),
    update_momentum=theano.shared(float32(0.9)),
    # ...
    )

The callback or list of callbacks that we pass will be called with two arguments: nn, which is the NeuralNet instance itself, and train_history, which is the same as nn.train_history_.

Instead of working with callback functions that use hard-coded values, we'll use a parametrizable class with a __call__ method as our callback. Let's call this class AdjustVariable. The implementation is reasonably straight-forward:

class AdjustVariable(object):
    def __init__(self, name, start=0.03, stop=0.001):
        self.name = name
        self.start, self.stop = start, stop
        self.ls = None

    def __call__(self, nn, train_history):
        if self.ls is None:
            self.ls = np.linspace(self.start, self.stop, nn.max_epochs)

        epoch = train_history[-1]['epoch']
        new_value = float32(self.ls[epoch - 1])
        getattr(nn, self.name).set_value(new_value)

Let's plug it all together now and then we're ready to start training:

net4 = NeuralNet(
    # ...
    update_learning_rate=theano.shared(float32(0.03)),
    update_momentum=theano.shared(float32(0.9)),
    # ...
    regression=True,
    # batch_iterator_train=FlipBatchIterator(batch_size=128),
    on_epoch_finished=[
        AdjustVariable('update_learning_rate', start=0.03, stop=0.0001),
        AdjustVariable('update_momentum', start=0.9, stop=0.999),
        ],
    max_epochs=3000,
    verbose=1,
    )

X, y = load2d()
net4.fit(X, y)

with open('net4.pickle', 'wb') as f:
    pickle.dump(net4, f, -1)

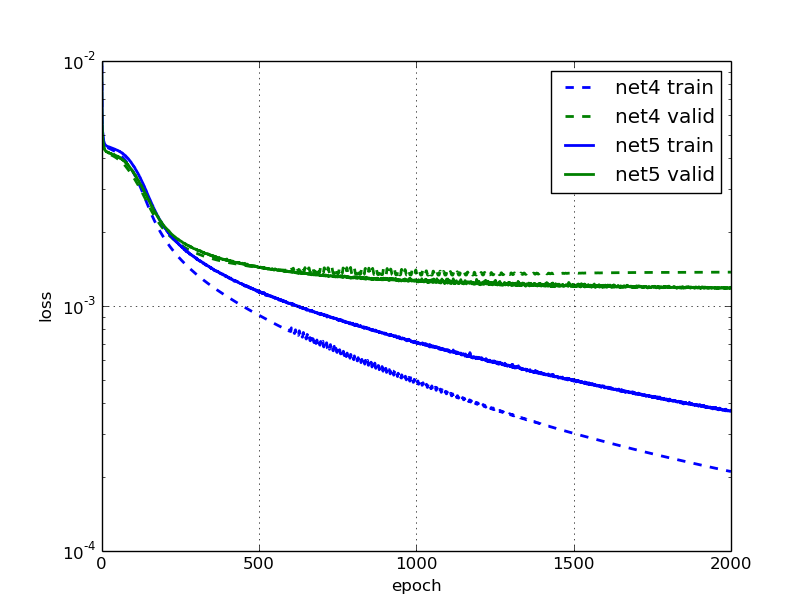
We'll train two nets: net4 doesn't use our FlipBatchIterator, net5 does. Other than that, they're identical.

This is the learning of net4:

 Epoch  |  Train loss  |  Valid loss  |  Train / Val
--------|--------------|--------------|----------------
    50  |    0.004216  |    0.003996  |     1.055011
   100  |    0.003533  |    0.003382  |     1.044791
   250  |    0.001557  |    0.001781  |     0.874249
   500  |    0.000915  |    0.001433  |     0.638702
   750  |    0.000653  |    0.001355  |     0.481806
  1000  |    0.000496  |    0.001387  |     0.357917

Cool, training is happening much faster now! The train error at epochs 500 and 1000 is half of what it used to be in net2, before our adjustments to learning rate and momentum. This time, generalization seems to stop improving after 750 or so epochs already; looks like there's no point in training much longer.

What about net5 with the data augmentation switched on?

 Epoch  |  Train loss  |  Valid loss  |  Train / Val
--------|--------------|--------------|----------------
    50  |    0.004317  |    0.004081  |     1.057609
   100  |    0.003756  |    0.003535  |     1.062619
   250  |    0.001765  |    0.001845  |     0.956560
   500  |    0.001135  |    0.001437  |     0.790225
   750  |    0.000878  |    0.001313  |     0.668903
  1000  |    0.000705  |    0.001260  |     0.559591
  1500  |    0.000492  |    0.001199  |     0.410526
  2000  |    0.000373  |    0.001184  |     0.315353

And again we have much faster training than with net3, and better results. After 1000 epochs, we're better off than net3 was after 3000 epochs. What's more, the model trained with data augmentation is now about 10% better with regard to validation error than the one without.

Dropout

Introduced in 2012 in the Improving neural networks by preventing co-adaptation of feature detectors paper, dropout is a popular regularization technique that works amazingly well. I won't go into the details of why it works so well, you can read about that elsewhere.

Like with any other regularization technique, dropout only makes sense if we have a network that's overfitting, which is clearly the case for the net5 network that we trained in the previous section. It's important to remember to get your net to train nicely and overfit first, then regularize.

To use dropout with Lasagne, we'll add DropoutLayer layers between the existing layers and assign dropout probabilities to each one of them. Here's the complete definition of our new net. I've added a # ! comment at the end of those lines that were added between this and net5.

net6 = NeuralNet(
    layers=[
        ('input', layers.InputLayer),
        ('conv1', layers.Conv2DLayer),
        ('pool1', layers.MaxPool2DLayer),
        ('dropout1', layers.DropoutLayer),  # !
        ('conv2', layers.Conv2DLayer),
        ('pool2', layers.MaxPool2DLayer),
        ('dropout2', layers.DropoutLayer),  # !
        ('conv3', layers.Conv2DLayer),
        ('pool3', layers.MaxPool2DLayer),
        ('dropout3', layers.DropoutLayer),  # !
        ('hidden4', layers.DenseLayer),
        ('dropout4', layers.DropoutLayer),  # !
        ('hidden5', layers.DenseLayer),
        ('output', layers.DenseLayer),
        ],
    input_shape=(None, 1, 96, 96),
    conv1_num_filters=32, conv1_filter_size=(3, 3), pool1_pool_size=(2, 2),
    dropout1_p=0.1,  # !
    conv2_num_filters=64, conv2_filter_size=(2, 2), pool2_pool_size=(2, 2),
    dropout2_p=0.2,  # !
    conv3_num_filters=128, conv3_filter_size=(2, 2), pool3_pool_size=(2, 2),
    dropout3_p=0.3,  # !
    hidden4_num_units=500,
    dropout4_p=0.5,  # !
    hidden5_num_units=500,
    output_num_units=30, output_nonlinearity=None,

    update_learning_rate=theano.shared(float32(0.03)),
    update_momentum=theano.shared(float32(0.9)),

    regression=True,
    batch_iterator_train=FlipBatchIterator(batch_size=128),
    on_epoch_finished=[
        AdjustVariable('update_learning_rate', start=0.03, stop=0.0001),
        AdjustVariable('update_momentum', start=0.9, stop=0.999),
        ],
    max_epochs=3000,
    verbose=1,
    )

Our network is sufficiently large now to crash Python's pickle with a maximum recursion error. Therefore we have to increase Python's recursion limit before we save it:

import sys
sys.setrecursionlimit(10000)

X, y = load2d()
net6.fit(X, y)

import cPickle as pickle
with open('net6.pickle', 'wb') as f:
    pickle.dump(net6, f, -1)

Taking a look at the learning, we notice that it's become slower again, and that's expected with dropout, but eventually it will outperform net5:

 Epoch  |  Train loss  |  Valid loss  |  Train / Val
--------|--------------|--------------|---------------
    50  |    0.004619  |    0.005198  |     0.888566
   100  |    0.004369  |    0.004182  |     1.044874
   250  |    0.003821  |    0.003577  |     1.068229
   500  |    0.002598  |    0.002236  |     1.161854
  1000  |    0.001902  |    0.001607  |     1.183391
  1500  |    0.001660  |    0.001383  |     1.200238
  2000  |    0.001496  |    0.001262  |     1.185684
  2500  |    0.001383  |    0.001181  |     1.171006
  3000  |    0.001306  |    0.001121  |     1.164100

Also overfitting doesn't seem to be nearly as bad. Though we'll have to be careful with those numbers: the ratio between training and validation has a slightly different meaning now since the train error is evaluated with dropout, whereas the validation error is evaluated without dropout. A more comparable value for the train error is this:

from sklearn.metrics import mean_squared_error
print mean_squared_error(net6.predict(X), y)
# prints something like 0.0010073791

In our previous model without dropout, the error on the train set was 0.000373. So not only does our dropout net perform slightly better, it overfits much less than what we had before. That's great news, because it means that we can expect even better performance when we make the net larger (and more expressive). And that's what we'll try next: we increase the number of units in the last two hidden layers from 500 to 1000. Update these lines:

net7 = NeuralNet(
    # ...
    hidden4_num_units=1000,  # !
    dropout4_p=0.5,
    hidden5_num_units=1000,  # !
    # ...
    )

The improvement over the non-dropout layer is now becoming more substantial:

 Epoch  |  Train loss  |  Valid loss  |  Train / Val
--------|--------------|--------------|---------------
    50  |    0.004756  |    0.007043  |     0.675330
   100  |    0.004440  |    0.005321  |     0.834432
   250  |    0.003974  |    0.003928  |     1.011598
   500  |    0.002574  |    0.002347  |     1.096366
  1000  |    0.001861  |    0.001613  |     1.153796
  1500  |    0.001558  |    0.001372  |     1.135849
  2000  |    0.001409  |    0.001230  |     1.144821
  2500  |    0.001295  |    0.001146  |     1.130188
  3000  |    0.001195  |    0.001087  |     1.099271

And we're still looking really good with the overfitting! My feeling is that if we increase the number of epochs to train, this model might become even better. Let's try it:

net12 = NeuralNet(
    # ...
    max_epochs=10000,
    # ...
    )

 Epoch  |  Train loss  |  Valid loss  |  Train / Val
--------|--------------|--------------|---------------
    50  |    0.004756  |    0.007027  |     0.676810
   100  |    0.004439  |    0.005321  |     0.834323
   500  |    0.002576  |    0.002346  |     1.097795
  1000  |    0.001863  |    0.001614  |     1.154038
  2000  |    0.001406  |    0.001233  |     1.140188
  3000  |    0.001184  |    0.001074  |     1.102168
  4000  |    0.001068  |    0.000983  |     1.086193
  5000  |    0.000981  |    0.000920  |     1.066288
  6000  |    0.000904  |    0.000884  |     1.021837
  7000  |    0.000851  |    0.000849  |     1.002314
  8000  |    0.000810  |    0.000821  |     0.985769
  9000  |    0.000769  |    0.000803  |     0.957842
 10000  |    0.000760  |    0.000787  |     0.966583

So there you're witnessing the magic that is dropout. :-)

Let's compare the nets we trained so for and their respective train and validation errors:

 Name  |   Description    |  Epochs  |  Train loss  |  Valid loss
-------|------------------|----------|--------------|--------------
 net1  |  single hidden   |     400  |    0.002244  |    0.003255
 net2  |  convolutions    |    1000  |    0.001079  |    0.001566
 net3  |  augmentation    |    3000  |    0.000678  |    0.001288
 net4  |  mom + lr adj    |    1000  |    0.000496  |    0.001387
 net5  |  net4 + augment  |    2000  |    0.000373  |    0.001184
 net6  |  net5 + dropout  |    3000  |    0.001306  |    0.001121
 net7  |  net6 + epochs   |   10000  |    0.000760  |    0.000787

Training specialists

Remember those 70% of training data that we threw away in the beginning? Turns out that's a very bad idea if we want to get a competitive score in the Kaggle leaderboard. There's quite a bit of variance in those 70% of data and in the challenge's test set that our model hasn't seen yet.

So instead of training a single model, let's train a few specialists, with each one predicting a different set of target values. We'll train one model that only predicts left_eye_center and right_eye_center, one only for nose_tip and so on; overall, we'll have six models. This will allow us to use the full training dataset, and hopefully get a more competitive score overall.

The six specialists are all going to use exactly the same network architecture (a simple approach, not necessarily the best). Because training is bound to take much longer now than before, let's think about a strategy so that we don't have to wait for max_epochs to finish, even if the validation error stopped improving much earlier. This is called early stopping, and we'll write another on_epoch_finished callback to take care of that. Here's the implementation:

class EarlyStopping(object):
    def __init__(self, patience=100):
        self.patience = patience
        self.best_valid = np.inf
        self.best_valid_epoch = 0
        self.best_weights = None

    def __call__(self, nn, train_history):
        current_valid = train_history[-1]['valid_loss']
        current_epoch = train_history[-1]['epoch']
        if current_valid < self.best_valid:
            self.best_valid = current_valid
            self.best_valid_epoch = current_epoch
            self.best_weights = nn.get_all_params_values()
        elif self.best_valid_epoch + self.patience < current_epoch:
            print("Early stopping.")
            print("Best valid loss was {:.6f} at epoch {}.".format(
                self.best_valid, self.best_valid_epoch))
            nn.load_params_from(self.best_weights)
            raise StopIteration()

You can see that there's two branches inside the __call__: the first where the current validation score is better than what we've previously seen, and the second where the best validation epoch was more than self.patience epochs in the past. In the first case we store away the weights:

          self.best_weights = nn.get_all_params_values()

In the second case, we set the weights of the network back to those best_weights before raising StopIteration, signalling to NeuralNet that we want to stop training.

          nn.load_params_from(self.best_weights)
          raise StopIteration()

Let's update the list of on_epoch_finished handlers in our net's definition and use EarlyStopping:

net8 = NeuralNet(
    # ...
    on_epoch_finished=[
        AdjustVariable('update_learning_rate', start=0.03, stop=0.0001),
        AdjustVariable('update_momentum', start=0.9, stop=0.999),
        EarlyStopping(patience=200),
        ],
    # ...
    )

So far so good, but how would we go about defining those specialists and what they should each predict? Let's make a list for that:

SPECIALIST_SETTINGS = [
    dict(
        columns=(
            'left_eye_center_x', 'left_eye_center_y',
            'right_eye_center_x', 'right_eye_center_y',
            ),
        flip_indices=((0, 2), (1, 3)),
        ),

    dict(
        columns=(
            'nose_tip_x', 'nose_tip_y',
            ),
        flip_indices=(),
        ),

    dict(
        columns=(
            'mouth_left_corner_x', 'mouth_left_corner_y',
            'mouth_right_corner_x', 'mouth_right_corner_y',
            'mouth_center_top_lip_x', 'mouth_center_top_lip_y',
            ),
        flip_indices=((0, 2), (1, 3)),
        ),

    dict(
        columns=(
            'mouth_center_bottom_lip_x',
            'mouth_center_bottom_lip_y',
            ),
        flip_indices=(),
        ),

    dict(
        columns=(
            'left_eye_inner_corner_x', 'left_eye_inner_corner_y',
            'right_eye_inner_corner_x', 'right_eye_inner_corner_y',
            'left_eye_outer_corner_x', 'left_eye_outer_corner_y',
            'right_eye_outer_corner_x', 'right_eye_outer_corner_y',
            ),
        flip_indices=((0, 2), (1, 3), (4, 6), (5, 7)),
        ),

    dict(
        columns=(
            'left_eyebrow_inner_end_x', 'left_eyebrow_inner_end_y',
            'right_eyebrow_inner_end_x', 'right_eyebrow_inner_end_y',
            'left_eyebrow_outer_end_x', 'left_eyebrow_outer_end_y',
            'right_eyebrow_outer_end_x', 'right_eyebrow_outer_end_y',
            ),
        flip_indices=((0, 2), (1, 3), (4, 6), (5, 7)),
        ),
    ]

We already discussed the need for flip_indices in the Data augmentation section. Remember from section The data that our load_data() function takes an optional list of columns to extract. We'll make use of this feature when we fit the specialist models in a new function fit_specialists():

from collections import OrderedDict
from sklearn.base import clone

def fit_specialists():
    specialists = OrderedDict()

    for setting in SPECIALIST_SETTINGS:
        cols = setting['columns']
        X, y = load2d(cols=cols)

        model = clone(net)
        model.output_num_units = y.shape[1]
        model.batch_iterator_train.flip_indices = setting['flip_indices']
        # set number of epochs relative to number of training examples:
        model.max_epochs = int(1e7 / y.shape[0])
        if 'kwargs' in setting:
            # an option 'kwargs' in the settings list may be used to
            # set any other parameter of the net:
            vars(model).update(setting['kwargs'])

        print("Training model for columns {} for {} epochs".format(
            cols, model.max_epochs))
        model.fit(X, y)
        specialists[cols] = model

    with open('net-specialists.pickle', 'wb') as f:
        # we persist a dictionary with all models:
        pickle.dump(specialists, f, -1)

There's nothing too spectacular happening here. Instead of training and persisting a single model, we do it with a list of models that are saved in a dictionary that maps columns to the trained NeuralNet instances. Now despite our early stopping, this will still take forever to train (though by forever I don't mean Google-forever, I mean maybe half a day on a single GPU); I don't recommend that you actually run this.

We could of course easily parallelize training these specialist nets across GPUs, but maybe you don't have the luxury of access to a box with multiple CUDA GPUs. In the next section we'll talk about another way to cut down on training time. But let's take a look at the results of fitting these expensive to train specialists first:

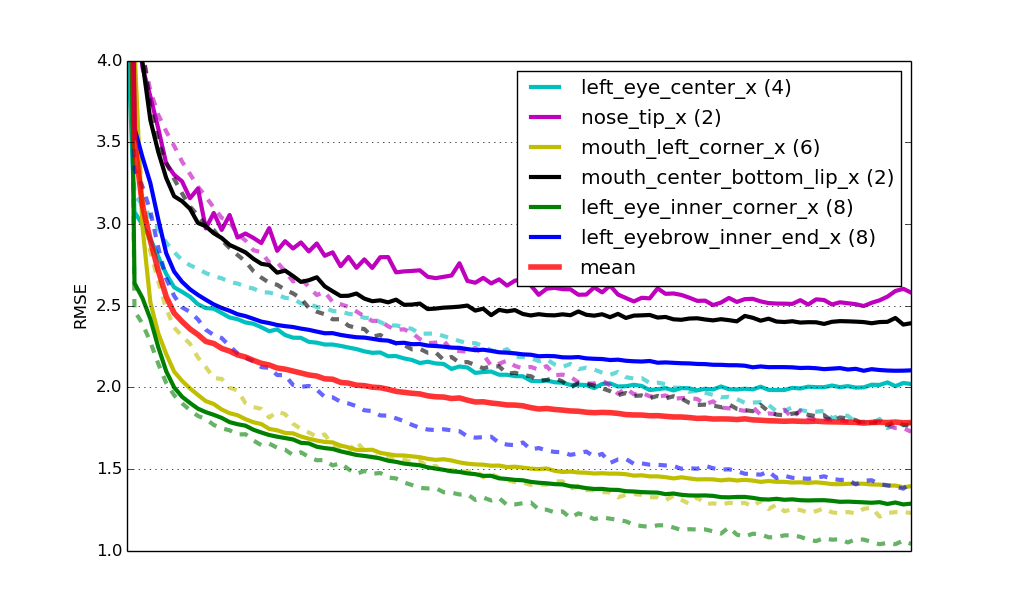
Learning curves for six specialist models. The solid lines represent RMSE on the validation set, the dashed lines errors on the train set. mean is the mean validation error of all nets weighted by number of target values. All curves have been scaled to have the same length on the x axis.

Lastly, this solution gives us a Kaggle leaderboard score of 2.17 RMSE, which corresponds to the second place at the time of writing (right behind yours truly).

Supervised pre-training

In the last section of this tutorial, we'll discuss a way to make training our specialists faster. The idea is this: instead of initializing the weights of each specialist network at random, we'll initialize them with the weights that were learned in net6 or net7. Remember from our EarlyStopping implementation that copying weights from one network to another is as simple as using the load_params_from() method. Let's modify the fit_specialists method to do just that. I'm again marking the lines that changed compared to the previous implementation with a # ! comment:

def fit_specialists(fname_pretrain=None):
    if fname_pretrain:  # !
        with open(fname_pretrain, 'rb') as f:  # !
            net_pretrain = pickle.load(f)  # !
    else:  # !
        net_pretrain = None  # !

    specialists = OrderedDict()

    for setting in SPECIALIST_SETTINGS:
        cols = setting['columns']
        X, y = load2d(cols=cols)

        model = clone(net)
        model.output_num_units = y.shape[1]
        model.batch_iterator_train.flip_indices = setting['flip_indices']
        model.max_epochs = int(4e6 / y.shape[0])
        if 'kwargs' in setting:
            # an option 'kwargs' in the settings list may be used to
            # set any other parameter of the net:
            vars(model).update(setting['kwargs'])

        if net_pretrain is not None:  # !
            # if a pretrain model was given, use it to initialize the
            # weights of our new specialist model:
            model.load_params_from(net_pretrain)  # !

        print("Training model for columns {} for {} epochs".format(
            cols, model.max_epochs))
        model.fit(X, y)
        specialists[cols] = model

    with open('net-specialists.pickle', 'wb') as f:
        # this time we're persisting a dictionary with all models:
        pickle.dump(specialists, f, -1)

It turns out that initializing those nets not at random, but by re-using weights from one of the networks we learned earlier has in fact two big advantages: One is that training converges much faster; maybe four times faster in this case. The second advantage is that it also helps get better generalization; pre-training acts as a regularizer. Here's the same learning curves as before, but now for the pre-trained nets:

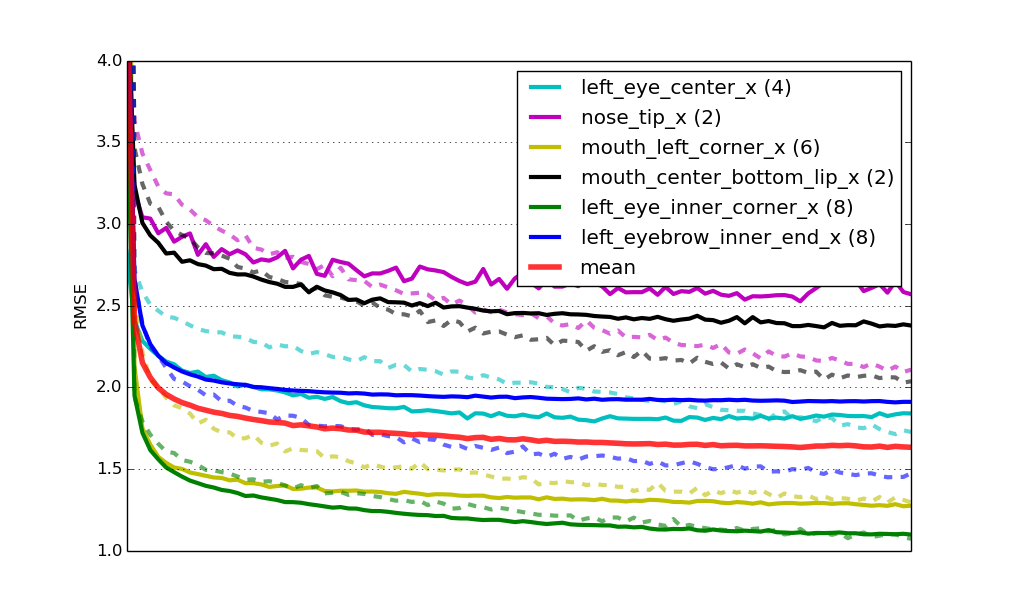
Learning curves for six specialist models that were pre-trained.

Finally, the score for this solution on the challenge's leaderboard is 2.13 RMSE. Again the second place, but getting closer!

Conclusion

There's probably a dozen ideas that you have that you want to try out. You can find the source code for the final solution here to download and play around with. It also includes the bit that generates a submission file for the Kaggle challenge. Run python kfkd.py to find out how to use the script on the command-line.

Here's a couple of the more obvious things that you could try out at this point: Try optimizing the parameters for the individual specialist networks; this is something that we haven't done so far. Observe that the six nets that we trained all have different levels of overfitting. If they're not or hardly overfitting, like for the green and the yellow net above, you could try to decrease the amount of dropout. Likewise, if it's overfitting badly, like the black and purple nets, you could try increasing the amount of dropout. In the definition of SPECIALIST_SETTINGS we can already add some net-specific settings; so say we wanted to add more regularization to the second net, then we could change the second entry of the list to look like so:

    dict(
        columns=(
            'nose_tip_x', 'nose_tip_y',
            ),
        flip_indices=(),
        kwargs=dict(dropout2_p=0.3, dropout3_p=0.4),  # !
        ),

And there's a ton of other things that you could try to tweak. Maybe you'll try adding another convolutional or fully connected layer? I'm curious to hear about improvements that you're able to come up with in the comments.

Edit: Kaggle features this tutorial on their site where they've included instructions on how to use Amazon GPU instances to run the tutorial, which is useful if you don't own a CUDA-capable GPU.